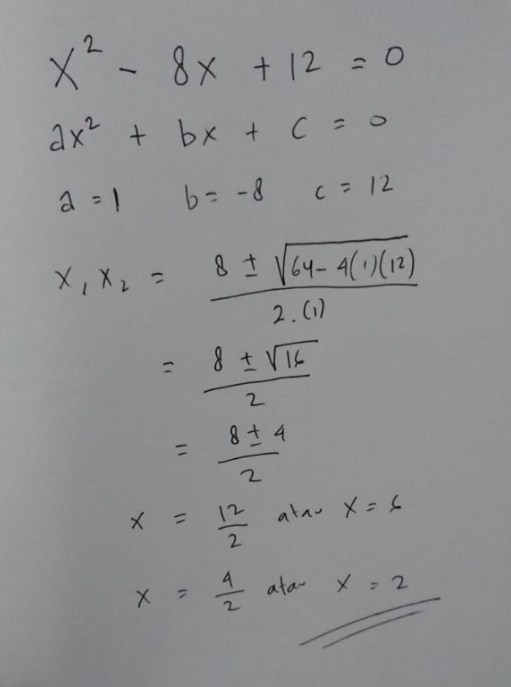Tentukan Akar Persamaan Kuadrat Berikut Dengan Cara Melengkapkan Kuadrat Sempurna X2 16 0

X 2 8x 9 0 x 2 8x 9 x 2 8x 16 9 16 x 2 8x 16 25 x 4 2 25 x 4 25 x 4 5 x 4 5 x 1 atau x 4.

Tentukan akar persamaan kuadrat berikut dengan cara melengkapkan kuadrat sempurna x2 16 0. Metode melengkapkan kuadrat sempurna akan mudah digunakan jika koefisien a dibuat agar bernilai 1. X 5x 24 0 4 tentukan nilai a b dan c dari persamaan kuadrat berikut. 9x 16x 13 0 3 gunakan rumus abc untuk mencari akar akar persamaan kuadrat berikut. X 1 3.

Misalnya terdapat sebuah persamaan berbentuk ax 2 bx c 0 dengan a b c r dan a 0. Diubah bentuk menjadi persamaan. X 7x 12 0 b. 2x 5x 21 0 b.

2 tentukan akar akar persamaan kuadrat berikut dengan cara melengkapkan kuadrat sempurna. Dengan menggunakan rumus akar akar akar persamaan kuadrat ax 2 bx c 0 adalah sebagai berikut. Tetapi ada satu hal yang perlu. Berdasarkan proses di atas kita bisa menyimpulkan langkah langkah dalam menentukan akar akar persamaan kuadrat dengan cara melengkapkan kuadrat sempurna.

X 2 2 2x 5 2 dan 3x 2 merupakan contoh bentuk kuadrat sempurna. Tujuan akhirnya kita mendapatkan bentuk x p 2 q sehingga untuk mendapatkan nilai x menjadi lebih mudah. Maka dengan melengkapkan kuadrat sempurna akar akarnya dapat dicari langkah langkah berikut. Bentuk persamaan kuadrat hingga koefisien kuadrat menjadi 1.

Nilai dari konstanta p dan q dari persamaan. Metode rumus abc ini. Perubahan tersebut dapat dibuktikan sebagai berikut. Misalkan kita memiliki bentuk umum persamaan kuadrat ax 2 bx c 0.

Maka dengan melengkapkan kuadrat sempurna akar akarnya dapat dicari langkah langkah berikut. Bilangan kuadrat sempurna merupakan bilangan yang jika diakarkan akan menghasilkan bilangan asli. 8x separuhnya 8 adalah 4 angka yang akan ditambahkan adalah 4 2 16 sehingga. Sekarang kita buktikan rumus tersebut dengan menggunakan metode melengkapkan kuadrat sempurna.

Cara ini jika tidak terbiasa bisa dibilang susah. Pk dalam bentuk. Selain metode pemfaktoran salah satu cara yang dapat kita gunakan untuk menentukan akar akar suatu persamaan kuadrat adalah dengan cara melengkapkan bentuk kuadrat sempurna. Misalnya terdapat sebuah persamaan berbentuk ax 2 bx c 0 dengan a b c r dan a 0.

Berikut ini adalah langkah langkah dalam menentukan akar akar persamaan kuadrat dengan cara melengkapkan kuadrat sempurna. Jika akar akar persamaan kuadratnya dengan jumlah dan kali x1 dan x2 telah diketahui maka persamaan kuadratnya dapat diubah dalam bentuk sebagai berikut. Jika proses untuk memperoleh persamaan kuadrat di atas kita balik maka akan diperoleh cara menyelesaikan persamaan kuadrat yang disebut melengkapkan kuadrat sempurna begin aligned x 2 8x 7 0 x 2 8x 7 x 2 8x 16 7 16 x 2 8x 16 9 x 4 2 9 end aligned sampai di sini kita bisa memperoleh akar akar persamaan kuadrat di atas. X 2 x 1 x 2 x x 1.

X 5x 5 0 b 2x. Tentukan persamaan kuadrat yang memiliki akar 3 dan 1 2. Berikut langkah langkah yang harus dilakukan. Dengan p dan q adalah konstanta serta x adalah variabel.