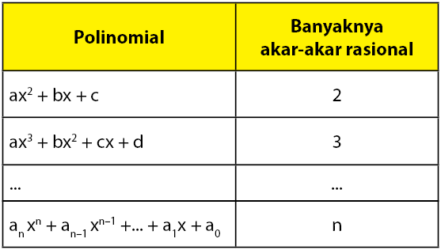
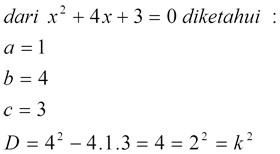Tentukan Akar Akar Rasional

Persamaan 6 tergolong persamaan linear. Bentuk akar merupakan bentuk lain untuk menyatakan bilangan berpangkat. Pertama pilih bilangan k yang tepat pilih k 1.

cabang akar akar lateral terbentuk dari pembelahan sel sel adalah biaya cabut akar gigi geraham bawah bibit akar wangi garut cabut sisa akar gigi geraham cara gampang mencari akar pangkat 3 cabang akar pada tumbuhan dikotil muda tumbuh dari daerah bilangan 6 per akar 2 jika dirasionalkan penyebutnya adalah buatlah algoritma mencari akar akar persamaan kuadrat dengan flowchart

Tentukan Akar Akar Rasional Dari Setiap Persamaan Sukubanyak Berikut Brainly Co Id

Contoh Soal Dan Pembahasan Menentukan Akar Akar Rasional Persamaan Suku Banyak Sukubanyak Math Youtube

Akar Akar Rasional Persamaan Suku Banyak Youtube

Banyaknya Akar Akar Rasional Dari X 4 X 3 11x 2 27x 36 Adalah Brainly Co Id

Tentukan Akar Akar Persamaan X3 2x2 5x 6 0 Brainly Co Id

Persamaan Kuadrat Yang Memiliki Akar Akar Rasional Adalah Tolong Di Jawab Ya Pliss Brainly Co Id

Akar akar suatu suku banyak dapat diperoleh dengan cara memfaktorkan suku banyak tersebut.

Tentukan akar akar rasional. Nah bilangan bilangan inilah yang disebut bentuk akar. Tulislah terlebih dulu untuk membuat nol pada garis bilangan dan tentukan juga tandanya untuk tiap tiap interval pada garis bilangan tersebut. Dan pada akar akar persamaan kuadrat yang didapat yaitu pembuat nol. Misalkan kita memiliki persamaan suku banyak sebagai berikut.

Definisi di atas memiliki arti bahwa tidak setiap bilangan yang dibubuhi tanda akar merupakan bentuk akar. Akar akar suatu suku banyak merupakan nilai yang menyebabkan suku banyak tersebut bernilai nol. Baik pembilang atau penyebut dikali dengan bentuk akar pada penyebut pecahan. Perhatikan akar dari bilangan bilangan berikut ini.

Hubungan akar dengan pangkat. Tentukan akar akar persamaan polinomial berderajat 3 di bawah. Nilai a o 48 jadi suku banyak tidak memiliki akar bernilai 0. Bentuk akar adalah akar dari bilangan rasional yang hasilnya merupakan bilangan irasional.

Bentuk akar merupakan akar dari suatu bilangan yang hasilnya bukan bilangan rasional atau merupakan bilangan irasional. Tentukan akar akar rasional suku banyak. Sedangkan untuk contoh nomor 3 dan 5 memiliki bilangan rasional yang jika dikuadratkan masing masing akan menghasilkan 4 dan 625 yaitu berturut turut adalah 2 dan 25. Faktor dari suatu suku banyak f x berderajat 3 dapat ditentukan dengan cara horner.

X2 x 6 0 difaktorkan menjadi x 3 x 2 0. Penyelesaian dari persamaan kuadrat disebut akar akar persamaan kuadrat. 9 bukan bentuk akar karena 9 3 bilangan rasional. Suatu bilangan eksponesial yang berpangkat pecahan dapat diubah ke dalam bentuk akar.

X 4 7x 3 8x 2 28x 48 0. Persamaan 7 juga bukan persamaan irasional karena variabelnya tidak termuat dalam tanda akar. Perhatikan beberapa contoh berikut. Nilai pengganti tersebut mengubah kalimat terbuka persamaan kuadrat menjadi sebuah pernyataan yang bernilai benar.

Persamaan 7 merupakan persamaan rasional. Bentuk akar termasuk dalam bilangan irasional yakni bilangan yang tidak dapat dinyatakan dengan pecahan a b a dan b bilangan bulat a dan b 0. Sekarang perhatikan proses mencari akar akar persamaan suku banyak berderajat 3 pada contoh soal di bawah. Kunci dalam merasionalkan penyebut sebuah pecahan yang berbentuk akar secara umum tergantung dari bentuk penyebutnya.

Persamaan kuadratdapat diselesaikan dengan cara menentukan nilai pengganti x yang memenuhi persamaan tersebut. Persamaan 6 bukan termasuk persamaan irasional karena variabelnya tidak berada di dalam tanda akar. Jumlah koefisien 1 7 8 28 48 18 karena jumlah koefisien tidak 0 maka suku banyak tidak memiliki akar bernilai 1 jumlah koefisien x berpangkat genap 1 8 48 39. Anxn an 1xn 1 an 2xn 2 a2xn a1x ao 0 untuk mencari akar akar rasional suku banyak maka kita.

Perhatikan bahwa untuk mengubah penyebut yang asalahnya bentuk akar menjadi bilangan rasional dibutuhkan pengali.