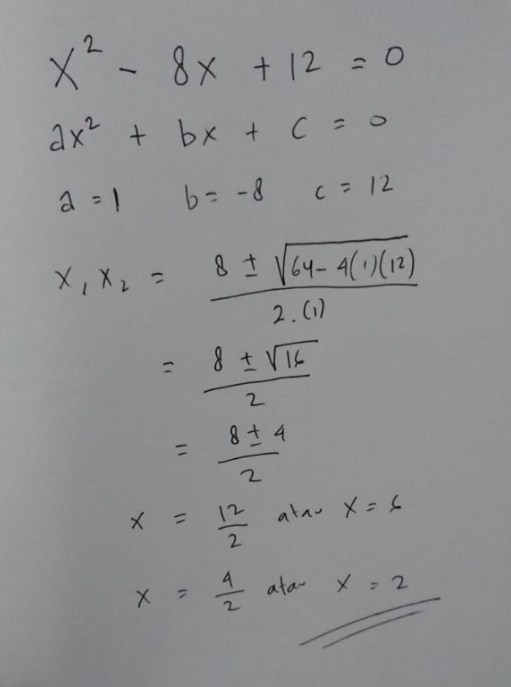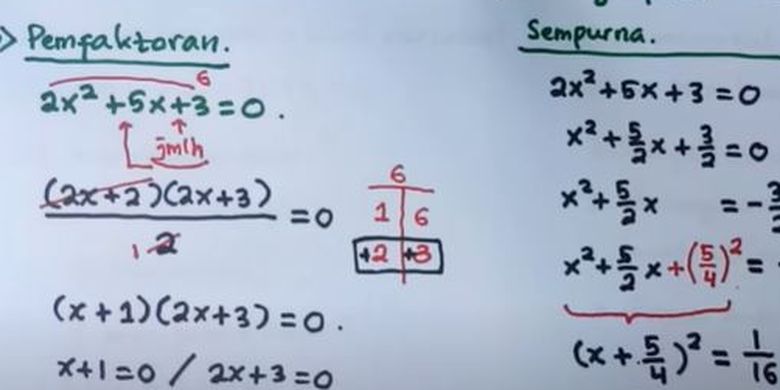Tentukan Akar Akar Persamaan Kuadrat Dengan Menggunakan Rumus Abc X2 16 0

Akar akar persamaan kuadrat x 2 5x 6 0 adalah.
Tentukan akar akar persamaan kuadrat dengan menggunakan rumus abc x2 16 0. Penyelesaian dari persamaan kuadrat disebut akar akar persamaan kuadrat. Salah satu metode yang unggul dalam menentukan akar akar persamaan kuadrat adalah dengan rumus kuadrat atau yang lebih dikenal sebagai rumus abc. Tentukan akar akar persamaan kuadrat x 8x 12 0 dengan menggunakan metode berikut. Pada artikel ini kami akan tunjukan belajar cara ketiga dengan menggunakan simple rumus abc.
1 dan 2 b. Menentukan akar akar persamaan kuadrat dengan rumus abc. Perhatikan contoh penggunaan rumus abc berikut. Faktorisasi pemfaktoran adalah suatu metode dalam mencari akar akar dengan mencari nilai yang jika dikalikan maka akan menghasilkan nilai lain.
Simak pembahasan soal dan jawabannya. Bahkan beberapa orang lebih memilih menggunakan cara ini sebagai cara utama tanpa melirik pemfaktoran ataupun melengkapkan bentuk kuadrat. Tentukan akar akar dari persamaan x 2 8x 12 0 dengan menggunakan rumus abc. Contoh penggunaan rumus abc.
Berikut ini penjelasan lengkap tentang persamaan kuadrat mulai dari konsep dasar menentukan akar akar rumus abc menyusun persamaan kuadrat baru contoh soal. Persamaan kuadratdapat diselesaikan dengan cara menentukan nilai pengganti x yang memenuhi persamaan tersebut. Dalam tayangan hari ini siswa sma dan smk belajar menentukan akar persamaan kuadrat. Maka akar akar persamaan kuadrat adalah sebagai berikut.
Diantaranya yaitu faktorisasi kuadrat sempurna dan menggunakan rumus abc. Berikut penjelasan mengenai beberapa metode untuk mencari akar akar persamaan. Semua persamaan kuadrat dapat diselesaikan dengan rumus abc. Jadi akar akar persamaan kuadrat x 2 8x 12 0 adalah x1 6 atau x2 2 sehingga himpunan penyelesaiannya adalah hp 6 2 7.
Untuk menggunakan rumus abc sobat idschool hanya perlu substitusi nilai a b dan c ke dalam rumus abc. Rumus abc atau sering disebut rumus kuadrat biasanya digunakan untuk persamaan kuadrat yang sulit difaktorkan. Ada beberapa teknik yang dapat digunakan untuk mencari penyelesaian atau akar akar suatu persamaan kuadrat. Nilai pengganti tersebut mengubah kalimat terbuka persamaan kuadrat menjadi sebuah pernyataan yang bernilai benar.
Kelemahan dari teknik pemfaktoran adalah sulit diterapkan apabila akar akar. Tidak seperti metode pemfaktoran dan melengkapkan kuadrat sempurna penggunaan rumus abc tidak terbatas pada bentuk tertentu. Diketahui a 1 b 8 dan c 12. Salah satunya adalah dengan teknik pemfaktoran yang sudah pernah dimuat pada post saya terdahulu.