Akar Dari X Kuadrat 7 X 10 0

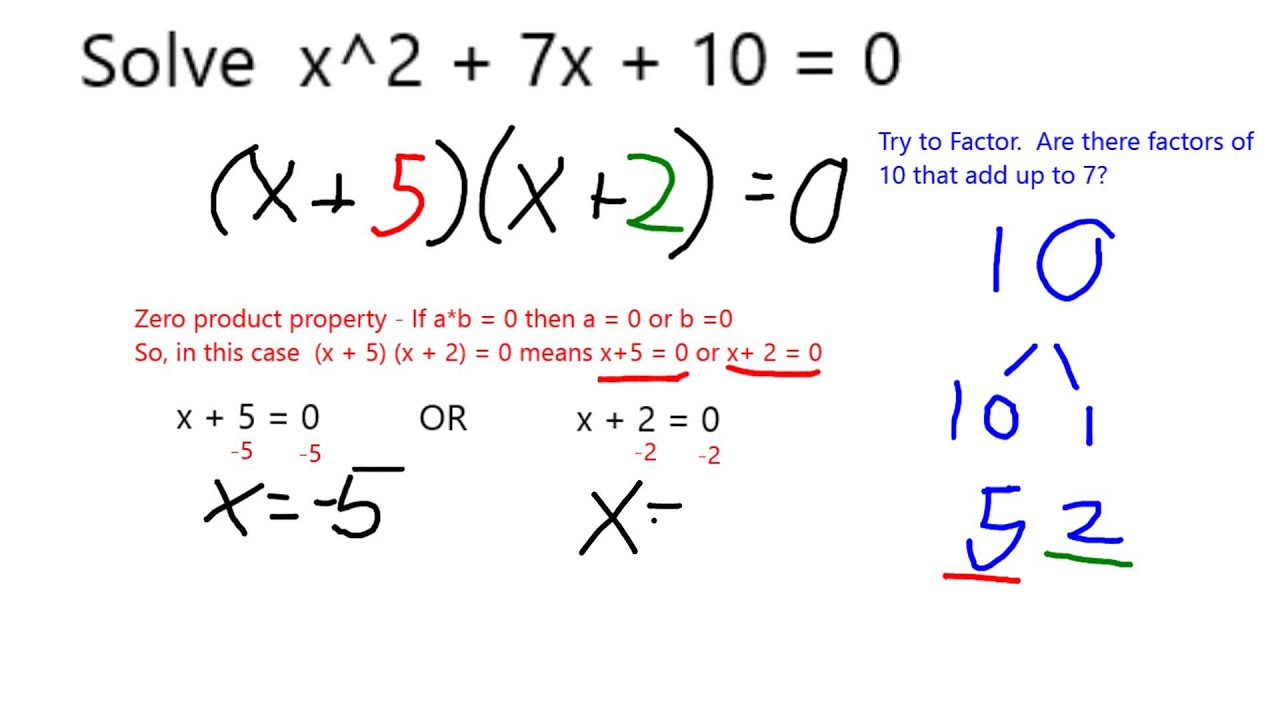
X 3 c.

Akar dari x kuadrat 7 x 10 0. Misalnya jika x 3 2 akan menghasilkan bentuk x 2 6x 9 atau x 2 6x 9 akan sama dengan x 3 2 sebagai gambaran awal diberikan soal untuk diselesaikan dengan cara melengkapkan kuadrat sempurna. X 2 0 x 2. X 2 6x 5 0 soal ini mirip dengan bentuk kuadrat sempurna yang sudah kita kenal pada pendahuluan di atas yaitu. Cara menurunkan akar kuadrat x.

Berikut macam macam akar persamaan kuadrat. Menentukan akar persamaan kuadrat. Selanjutnya kita tentukan akar akar dari pertidaksamaan dengan menggunakan rumus abc. 3 x 2 x 2 0.

X 5 b. Contoh persamaan akar real d 0 tentukan jenis akar persamaan dari persamaan x 2 4x 2 0. X 2 8 x 15. Himpunan penyelesaian dari pertidaksamaan kuadrat x 2 8x 15 0 untuk x r adalah.

Akar akar persamaan kuadrat yang didapat yaitu pembuat nol. X 2 0 x 2. Jika telah belajar kalkulus tentunya anda sudah mengetahui aturan pangkat untuk menemukan diferensial turunan fungsi dasar. Maka pembuat nolnya sudah didapat yaitu 3 dan 2.

X2 x 6 0 difaktorkan menjadi x 3 x 2 0. Pembuat nol dari persamaan tersebut dapat dicari dengan pakai cara ini. Kedua kita gunakan. Namun ketika fungsi berisi akar kuadrat atau tanda radikal misalnya sqrt x.

X 5 d. X 2 10 x 21. Yang kedua gunakanlah. Tentukan akar akar dari persamaan kuadrat x 2 5x 6 0 solusi.

Biar lebih lancar silahkan dicoba mencari akar persamaan kuadrat dari soal soal berikut ini. Dan pada akar akar persamaan kuadrat yang didapat yaitu pembuat nol. Contoh mencari akar persamaan kuadrat dengan cara memfaktorkannya terlebih dahulu adalah sebagai berikut. Langkah pertama yang harus kita lakukan adalah mensubstitusikan nilai x 3 untuk mengetahui nilai c.

Mencari akar persamaan kuadrat dengan rumus abc rumus kecap dalam beberapa soal sobat akar persamaan kuadrat kadang ada yang tidak bisa dicari. Akar real d 0 jika nilai d 0 dari suatu pk maka akan menghasilkan akar akar persamaan yang real namun memiliki akar akar yang berlainan. Dengan kata lain x1 tidak sama dengan x2. X 2 5x 6 0 x 2 3 2 x 6 0 x 2 3x 2x 6 0 x x 3 2 x 3 0 x 2 x 3 0 x 2 0 x 1 2 x 3 0 x 2 3 melengkapkan kuadrat sempurna metode ini dilakukan dengan mengubah persamaan kuadrat menjadi bentuk kuadrat sempurna secara paksa.

Yang pertama gunakanlah. X 3 0 x 3. Jadi pembuatan nolnya sudah didapatkan yaitu 3 dan 2. Persamaan kuadrat jika sudah dalam bentuk faktor faktor akarnya dapat dicari dengan cara membuat masing masing faktor sama dengan nol setelah itu cari nilai dari peubah x.

Apabila salah satu akar dari persamaan kuadrat x 2 2x c 0 yaitu 3 maka akar lainnya ialah. X2 x 6 0 difaktorkan menjadi x 3 x 2 0. X 2 2x 3 0 x 1 x 3 0 x 1 atau x 3. X 2 4x 12 0.

Jadi kita ketahui a 3 b 4 dan c 7. X 1 2.